No CrossRef data available.
Article contents
The mean-square value of the divisor function
Published online by Cambridge University Press: 14 June 2016
Extract
The behaviour of the divisor function d (n) is rather tricky. For a prime p, we have d(p) = 2, but if n is the product of the first k primes then, by Chebyshev's estimate for the prime counting function [1, Theorem 414], we have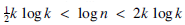 
so that
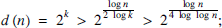
for such n then, d (n) is ‘unusually large’ — it can exceed any fixed power of log n, for example.
In [2] Jameson gives, amongst other things, a derivation of Dirichlet's theorem, which shows that the mean-value of the divisor function in an interval containing n is log n. However, the result is somewhat deceptive because, for most n, the value of d (n) is substantially smaller than log n.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
1.Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (4th edn.), Oxford (1960).Google Scholar
3.Ramanujan, S., Some formulae in the analytic theory of numbers, Messenger of Math. 45 (1916) pp. 81–84.Google Scholar
4.Wilson, B. M., Proofs of some formulae enunciated by Ramanujan, Proc. London Math. Soc. (2) 21 (1922) pp. 235–255.Google Scholar
5.Jia, Chaohua and Sankaranarayanan, Ayyadurai, The mean square of the divisor function, Ada Arith. (2) 164 (2014) pp. 181–208.CrossRefGoogle Scholar
6.Titchmarsh, E. C., The theory of the Riemann zeta-function (2nd edn.) Oxford (1986) (revised by Heath-Brown, D. R.).Google Scholar