Article contents
Lyness cycles
Published online by Cambridge University Press: 15 June 2017
Extract
In 1942, R. C. Lyness noted that some recurrence relations generate cycles, irrespective of the initial values. For example, the order 2 recurrence relation
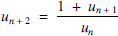
generates a cycle of period 5 for almost all values of u1 and u2 [1].
The globally periodic nature of sequences generated by this recurrence relation can be seen by setting u1 = x and u2 = y. The sequence is then
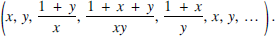
Lyness gave other examples of such recurrence relations but had been unable to find one with period 7 and challenged readers of the Gazette to find such a recurrence relation or prove it to be impossible.
No answer to this challenge was forthcoming. However, since Lyness's time, interest in these cycles has been maintained due to links with cross-ratios and elliptic curves. In recent years, Jonny Griffiths has done much to popularise these cycles [2].
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2017
References
- 2
- Cited by


