I feel that many of the descriptions of linear programming are either too elementary or else expressed in terms of n variables with m constraints using matrices and innumerable Σ's. This is an attempt to arrive at a description somewhere between the two and in it I take n = 7, m = 3.

Suppose that the function to be minimized is given by

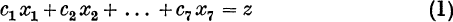
and that in addition to xq ≥ 0 for all q, the equations of constraint are

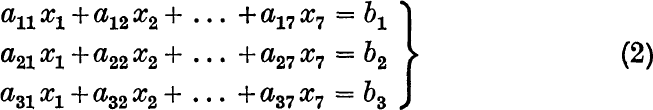
Solving equations (2) for any three of the variables, say x1, x2, x3, gives equations like

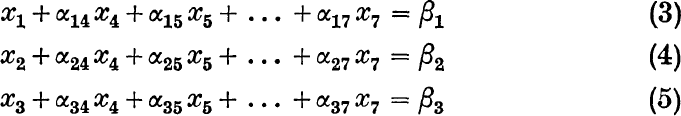
Suppose that solving for the variables x1, x2, x3 gives non-negative values of β1, β2, β3; if it does not, three other variables must be chosen until positive numbers are obtained on the right-hand side.