No CrossRef data available.
Published online by Cambridge University Press: 03 November 2016
It is well known that, if.
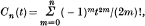
cos t>Cn(t) or cos t<Cn(t) holds for 0< t< ∞ according as n = 1, 3, 5, … or n = 2, 4, 6, …. It will be noted that this is not obvious in itself. In fact, the absolute values of the successive terms of the alternating series 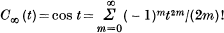 do not decrease from m = 0 onward, except when t is small.
do not decrease from m = 0 onward, except when t is small.