No CrossRef data available.
Published online by Cambridge University Press: 16 February 2023
In order to state our primary results, we must first establish some
notation. Let S-1 (x) = sin x and C-1 (x) = cos x, then for each non-negative integer n, let
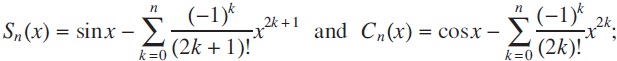
these are the remainders of the Maclaurin series for sine and cosine, respectively. Note that 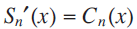 for each
for each  and
and 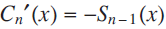 for each
for each 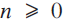 . It is known that
. It is known that
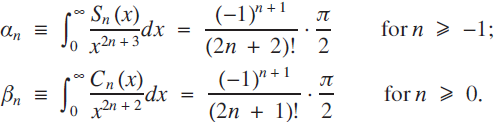
See [1] for several different proofs of the well-known fact that
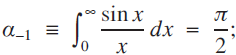
the values of αn and βn for 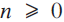 then follow rather easily using induction and integration by parts. (Details are provided in the Appendix.)
then follow rather easily using induction and integration by parts. (Details are provided in the Appendix.)