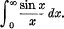Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T21:21:11.067Z Has data issue: false hasContentIssue false
  • English
  • Français

The Integral

Published online by Cambridge University Press:  03 November 2016

G. H. Hardy
Get access Rights & Permissions [Opens in a new window]

Extract

No one can possibly welcome more cordially than I do the widening of the school curriculum in mathematics that has taken place during the last twenty years. Even I can remember the days when “Conics” and “Mechanics” were the privilege of a select few, and only a prodigy was initiated into the mysteries of the Differential (much less the Integral) Calculus. All this is changed now, and it is fairly safe (at least that is my experience) to assume that a boy who has won a scholarship has learnt something about the Integral Calculus at school.

Type
2. Highlights
Information
The Mathematical Gazette , Volume 55 , Issue 392 , March 1971 , pp. 152 - 158
Copyright
Copyright © Mathematical Association 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* A. Berry, Messenger of Mathematics, vol. 37, p. 61; E. J. Nanson, ibid. p. 113.

† Whether this is true of a proof by “contour integration” depends logically on what proof of Cauchy’s Theorem has been used (see my remarks under 3 below).

‡ For an explanation of the general nature of a “double limit problem” see my Course of Pure Mathematics (App. 2, p. 420); for examples of the working out of such problems see Mr. Bromwich’s Infinite Series (passim, but especially App. 3, p. 414 et seq.).

§ I mean, of course, the first proof mentioned by Mr. Berry—the proof itself is classical.

* Forsyth, Theory of Functions, p. 23.

* Goursat’s proof is better and more general, and does not involve my inversion of limit-operations, but its difficulties are far too delicate for beginners.

* This proof is also referred to by Prof. Nanson. The only proofs which are “classical” are 1, 2, 3, viz. the three discussed by Mr. Berry.

* This I know to be Mr. Berry’s opinion. He would put 2 below 3 and 4, and 5 below 6. To compare 3 and 4 is very difficult, and they might fairly be bracketed.

Since writing this note I have recollected another proof which I had forgotten, and which is given in § 173 (Ex. 1) of Mr. Bromwich’s Infinite Series. Mr. Bromwich there proves that, provided the real parts of a and 6 are positive or zero,

Putting a = 1, b =i, we obtain

This proof, as presented by Mr. Bromwich, should be marked at about 45. It has the advantage of giving the values of several other interesting integrals as well, so that (as in the case of Prof. Nanson’s proof) it is hardly fair to contrast this mark with the considerably lower marks obtained by some of the other proofs.