Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T15:42:10.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalising ‘Sums of cubes equal to squares of sums’

Published online by Cambridge University Press:  01 August 2016

John Mason
John Mason*
Affiliation:
Faculty of Mathematics, The Open University, Milton Keynes MK7 6AA
Get access Rights & Permissions [Opens in a new window]

Extract

David Pagni drew attention to a result which is ascribed by Dickson [2, p. 286] to Liouville (1857), that the sum of the cubes of the number of divisors of each of the divisors of an integer, is equal to the square of their sum. For example, the divisors of 6 are 1, 2, 3, and 6, which have 1, 2, 2, and 4 divisors respectively, and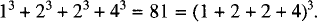

Pagni observed, as have others, including Mason et al. [4, p. 179], that the reason Liouville’s result works is because the numbers generated are element-by-element products of sequences of the form {1, 2, ..., t}, which are well known to have the sum of their cubes equal to the square of their sum.

Type
Articles
Information
The Mathematical Gazette , Volume 85 , Issue 502 , March 2001 , pp. 50 - 58
Copyright
Copyright © The Mathematical Association 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Pagni, David, An interesting number fact, Math. Gaz. 82 (July 1998) pp. 271–273.CrossRefGoogle Scholar
2. Dickson, L., History of the Theory of Numbers, Volume I Divisibility and Primality, Chelsea, New York (1910 republished 1971).Google Scholar
3. Liouville, J., Jour, de Mathématiques 2 (2) Comptes Rendus, Paris, pp. 425–432 in the fourth article of the series (1857).Google Scholar
4. Mason, J., Burton, L. and Stacey, K., Thinking Mathematically, Addison Weslev (1982)Google Scholar