Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T23:00:40.606Z Has data issue: false hasContentIssue false
  • English
  • Français

The gaps between sums of two squares

Published online by Cambridge University Press:  23 January 2015

Peter Shiu
Peter Shiu*
Affiliation:
353 Fulwood Road, Sheffield S10 3BQ e-mail:, [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Problems concerning the set

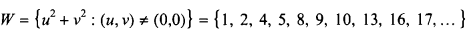
of numbers which are representable as sums of two squares have a long history. There are statements concerning W in the Arithmetic of Diophantus, who seemed to be aware of the famous identity

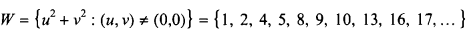
which shows that the set W is ‘multiplicatively closed’. Since a square must be congruent to 0 or 1 (mod 4), it follows that members of W cannot be congruent to 3 (mod 4). Also, it is not difficult to show that a number of the form 4k + 3 must have a prime divisor of the same form dividing it an exact odd number of times. However, the definitive statement (see, for example, Chapter V in [1]) concerning members of W, namely that they have the form PQ2, where P is free of prime divisors p ≡ 3 (mod 4), was first given only in 1625 by the Dutch mathematician Albert Girard. It was also given a little later by Fermat, who probably had a proof of it, but the first published proof was by Euler in 1749.

Type
Articles
Information
The Mathematical Gazette , Volume 97 , Issue 539 , July 2013 , pp. 256 - 262
Copyright
Copyright © The Mathematical Association 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Davenport, H., The higher arithmetic, Hutchinson's University Library, London (1952).Google Scholar
2. Shiu, P., Counting sums of two squares: the Meissel-Lehmer method, Math. Comp. 47 (1986) pp. 351–360.Google Scholar
3. Baker, R. C., Harman, G. and Pintz, J., The difference between consecutive primes. II', Proc. London Math. Soc. 83 (3) (2001) pp. 532–562.Google Scholar
4. Bambah, R. P. and Chowla, S., On numbers which can be expressed as a sum of two squares, Proc. Nat. Inst. Sci. India, 13 (1947) pp. 101–103.Google Scholar
5. Goldston, D. A., Pintz, J. and Yildirim, C. Y., Primes in tuples. I, Ann. of Math. 170 (2009) pp. 819–862.Google Scholar
6. Apostol, Tom M., Introduction to analytic number theory, Springer (1976).Google Scholar
7. Hall, M., Quadratic residues in factorisation, Bull. Amer. Math. Soc. 39 (1933) pp. 759–763.Google Scholar
8. Cobham, A., The recognition problem for perfect squares, Proc. 1966 IEEE Symposium on switching and automata theory, IEEE Press (1966) pp. 78–87.Google Scholar
9. Heath-Brown, D. R., Zero-free regions for Dirichlet L-functions, and the least prime in an arithmetic progression, Proc. London Math. Soc. 64 (3) (1992) pp. 265–338.Google Scholar