Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T18:35:27.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite groups, wallpaper patterns and non-euclidean geometries

Published online by Cambridge University Press:  22 September 2016

A. F. Beardon
A. F. Beardon*
Affiliation:
Department of Pure Mathematics, University of Cambridge, Mill Lane, Cambridge CB2 1SB
Get access Rights & Permissions [Opens in a new window]

Extract

Transformation geometry is now taught in many schools, and complex numbers are frequently used to describe the geometric transformations. For example, a translation is represented by 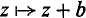(where b is a complex number), a rotation by 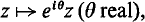a magnification by and a reflection in the x-axis by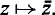

The set of all transformations of the form 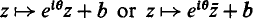forms a group and consists of precisely those transformations which preserve distance. Among the subgroups of this group there are the groups which give rise to the well known 17 distinct ‘wallpaper patterns’. These can be described in an elementary and geometric way and are (quite rightly) a popular topic in transformation geometry.

Type
Research Article
Information
The Mathematical Gazette , Volume 62 , Issue 422 , December 1978 , pp. 267 - 278
Copyright
Copyright © Mathematical Association 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Schwarzenberger, R. L. E., The 17 plane symmetry groups, Mathl Gaz. 58, 123–131 (No. 404, June 1974).Google Scholar
2. Budden, F. J., On functions which form a group, Mathl Gaz. 54, 9–18 (No. 387, February 1970).Google Scholar
3. Budden, F. J., Transformation geometry in the plane by complex number methods, Mathl Gaz. 53, 19–31 (No. 383, February 1969).Google Scholar
4. Burn, R. P., Geometrical illustrations of group-theoretical concepts, Mathl Gaz. 57, 110–119 (No. 400, June 1973).Google Scholar
5. Ford, L. R., Automorphic functions. Chelsea (1951).Google Scholar
6. Budden, F. J. The fascination of groups. Cambridge University Press (1972).Google Scholar
7. Weyl, H., Symmetry. Princeton University Press (1952).Google Scholar
8. Zassenhaus, H., The theory of groups. Chelsea (1949).Google Scholar
9. Magnus, W., Noneuclidean tessellations and their groups. Academic Press (1974).Google Scholar