Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-16T17:17:25.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast formulas for slowly convergent alternating series

Published online by Cambridge University Press:  23 January 2015

M.J. Cooker
M.J. Cooker*
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

One day the Tortoise was discussing with mighty Achilles the behaviour of infinite series. Achilles boasted that his mental powers were so fast that he could exhaust any series summation problem by simply adding up enough terms. But Tortoise was unimpressed:

‘Is that so? What's the sum of this series, then?’ With his tail he drew a line in the sand, and wrote

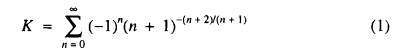
which is the same as

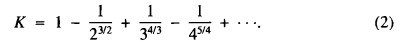
‘I'll give you until tomorrow to find K to four significant digits!’

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 533 , July 2011 , pp. 218 - 226
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Osler, T. J., A remarkable formula for approximating the sum of alternating series, Math. Gaz. 93 (March 2009) pp. 76–82.CrossRefGoogle Scholar
2. Borwein, J. M. and Borwein, P. B., π and the AGM, Wiley (1987).Google Scholar
3. Lord, N., Recent calculations of π:the Gauss-Salamin algorithm, Math. Gaz. 76, (July 1992) pp. 231–242.CrossRefGoogle Scholar
4. Bromwich, T. J. I'a, Introduction to the theory of infinite series (2nd edn.), Macmillan (1926).Google Scholar
5. Hartree, D. R., Numerical Analysis (2nd edn.), Clarendon Press (1958).Google Scholar
6. Lowry, H. V., Euler's transformation of alternating series, Math. Gaz. 31 (October 1947) pp. 249–250.CrossRefGoogle Scholar
7. Girling, A., Accelerating the convergence of an alternating series, Math. Gaz. 67 (October 1983) pp. 173–177.CrossRefGoogle Scholar
8. Sebah, P. and Gourdon, X., Convergence acceleration of series (2002) http://numbers.computation.free.fr/Constants/Miscellaneous/seriesacceleration.html Google Scholar
9. Cohen, H., Rodriguez Villegas, F. and Zagier, D., Convergence acceleration of alternating series, Experimental Mathematics 9(1) (2000) pp. 3–12.CrossRefGoogle Scholar
10. Murphy, Robin, Accelerating the convergence of some alternating series, Math. Gaz. 95 (March 2011) pp. 91–96.CrossRefGoogle Scholar