No CrossRef data available.
Published online by Cambridge University Press: 14 February 2019
There are recursive expressions (see [1]) for sequentially generating the integer solutions to Pell's equation: p2 − Dq2 = 1, where D is any positive non-square integer. With known positive integer solution p1 and q1 we can compute, using these recursive expressions, pn and qn for all n > 1. See Table in [2] for a list of smallest integer, or fundamental, solutions p1 and q1 for D≤ 128. These (pn, qn) pairs also form rational approximations to 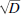 that, as noted in [3, Chapter 3], match with convergents (Cn = pn / qn) of the Regular Continued Fractions (RCF, continued fractions with the numerator of all fractions equal to 1) for
that, as noted in [3, Chapter 3], match with convergents (Cn = pn / qn) of the Regular Continued Fractions (RCF, continued fractions with the numerator of all fractions equal to 1) for 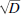 .
.