Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T00:42:47.082Z Has data issue: false hasContentIssue false
  • English
  • Français

The existence of triangles, tetrahedra, and higher-dimensional simplices with prescribed exradii

Published online by Cambridge University Press:  18 June 2018

Mowaffaq Hajja
Mowaffaq Hajja*
Affiliation:
Department of Basic Sciences and Mathematics, Philadelphia University, P. O. Box 1, 19392, Amman, Jordan e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

This Article is inspired by a problem that appeared recently in the American Mathematical Monthly, namely 11972 in [1, p. 369]. The problem asks the readers to prove that if r is the inradius of a tetrahedron, and if r1, r2, r3, r4 are its exradii, then

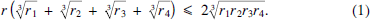
By taking r = r1 = r2 = r3 = r4 = 1, one sees that (1) is not true for all positive numbers r, r1, r2, r3, r4. This is not surprising, since r is dependent on r1, r2, r3, r4 by the elegant relation

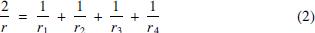
which we shall prove in Theorem 2 below; see also, for example, [2, (5), §266, p. 92], [3. §41, 2°, (1), p. 76] and [4, Problem 6′(i), p. 39]. Using this relation, one can rewrite (1) as

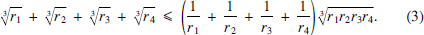
Intuitively, the four numbers r1, r2, r3, r4 are independent, and one may thus ask whether the inequality (3) holds for all positive numbers r1, r2, r3, r4 regardless of being the exradii of some tetrahedron or not.

Type
Articles
Information
The Mathematical Gazette , Volume 102 , Issue 554 , July 2018 , pp. 257 - 263
Copyright
Copyright © Mathematical Association 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Zhang, Y., Problem Proposal 11972, Amer. Math. Monthly 124 (4) (2017), p. 369.Google Scholar
2. Altshiller Court, N., Modern pure solid geometry (2nd edn.), Chelsea Publishing Company, New York (1964).Google Scholar
3. Couderc, P. et Balliccioni, A., Premier livre du tétraèdre, Gauthier-Villars, Editeurs, Paris (1935).Google Scholar
4. Miculita, M. and Brânzei, D., Analogii Triunghi-Tetraedru, Editura Paralela, Bucharest, Romania (2000).Google Scholar
5. Gerber, L., Associated and orthologic simplexes, Trans. Amer. Math. Soc. 231 (1977) pp. 47–63.Google Scholar
6. Gerber, L., Spheres tangent to all the faces of a simplex, J. Comb. Theory, Ser. A 12} (1972) pp. 453–456.CrossRefGoogle Scholar
7. Coxeter, H. S. M., Introduction to geometry (2nd edn.), John Wiley New York (1961).Google Scholar
8. Kay, D. C., College geometry, Holt, Rinehart, and Winston, Inc., New York (1969).Google Scholar
9. Leversha, G., The geometry of the triangle, Pathways, No. 2, The UK Mathematics Trust, University of Leeds, Leeds (2013).Google Scholar
10. Gerber, L., The orthocentric simplex as an extreme simplex, Pacific J. Math. 56 (1975) pp. 97–111.Google Scholar
11. Izumi, S., Sufficiency of simplex inequalities, Proc. Amer. Math. Soc. 144 (2016) pp. 1299–1307.Google Scholar
12. Mazur, M., Problem 10717, Amer. Math. Monthly 106 (1999) p. 167, 107 (2000) pp. 466–467.Google Scholar