No CrossRef data available.
Published online by Cambridge University Press: 03 November 2016
Consider a rigid body having one point O fixed, which is acted upon by a set of forces Fs (s = 1, 2, ..., n). Then the equation of motion of the body is given by
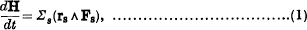
where H is the angular momentum of the body with respect to the point O and rs = OPs, Ps being the point of application of Fs. A similar equation holds in the general motion of a rigid body if H denotes the angular momentum with respect to G, its centre of gravity.
page 23 of note * In special types of motion, ![]() may coincide with a principal axis throughout the motion, but not i, as for instance in the steady precessional motion of a solid of revolution in rolling contact with a plane surface ; but in general this is not the case, and the condition for
may coincide with a principal axis throughout the motion, but not i, as for instance in the steady precessional motion of a solid of revolution in rolling contact with a plane surface ; but in general this is not the case, and the condition for ![]() to vanish is that i should coincide with a principal axis of inertia at a.
to vanish is that i should coincide with a principal axis of inertia at a.
page 23 of note † The above theory is clearly applicable to this motion provided there is no slipping at the point of contact.
page 26 of note * Since in the case when the spinning body is a sphere i is in the direction of the normal to the second surface at the point of contact, we shall in future refer to an integral involving the component of the angular velocities about the common normal as an integrsl of normal spin.
page 29 of note * The existence of the integral a(i . Ω) =constant, under the condition that Ω' is either zero or perpendicular to the plane, could also have been deduced, of course, as a direct consequence of the fact that during the motion the direction of i, and so of IG, is constant. (See (a), general result, p. 25.)