Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T07:32:18.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Emmental squares are tasty

Published online by Cambridge University Press:  08 February 2018

Tony Crilly ,
Stan Dolan  and
Colin R. Fletcher
Tony Crilly
Affiliation:
10 Lemsford Road, St Albans AL1 3PB e-mail: [email protected]
Stan Dolan
Affiliation:
126A Harpenden Road, St Albans AL3 6BZ e-mail: [email protected]
Colin R. Fletcher
Affiliation:
Atalaya, Lon Glanfred, Llandre, Aberystwyth SY24 5BY e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

A shape is called equable if its area and perimeter are numerically equal relative to some given system of units. For example, if a square is equable, then its side, a, must satisfy 4a = a2. So there is only one equable square, and it has side 4.

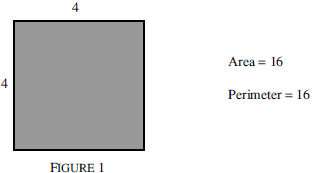
It is easy to investigate this idea for other shapes. Though not connected with this problem, the work of Imre Lakatos suggested a generalisation to us. Lakatos showed that Euler's classical formula V + F = E − 2 for polyhedra could be extended when the notion of tunnels was introduced [1].

Type
Articles
Information
The Mathematical Gazette , Volume 102 , Issue 553 , March 2018 , pp. 13 - 22
Copyright
Copyright © Mathematical Association 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Lakatos, I., Proofs and refutations: the logic of mathematical discovery, Cambridge University Press (1976).CrossRefGoogle Scholar
2. Conway, J. H., ‘Mrs. Perkins’ Quilt’, Mathematical Proceedings of the Cambridge Philosophical Society, 60 (1964), pp. 363–368.CrossRefGoogle Scholar
3. Tutte, W. T., Squaring the square, Scientific American 199 (5) (November 1958) pp. 136–142.Google Scholar
4. Erdős, P., Graham, R. L., On packing squares with equal squares. Journal of Combinatorial Theory, Series A, 19 (1975), pp. 119–123.CrossRefGoogle Scholar
5. Dolan, S., Thoughts on a conjecture of Erdős, Math. Gaz. 101 (November, 2017) pp. 449–457.CrossRefGoogle Scholar