No CrossRef data available.
Article contents
Droz-Farny constructions
Published online by Cambridge University Press: 23 January 2015
Extract
Notation: If A, B are points, then AB denotes the line AB rather than just the segment from A to B, unless stated otherwise. If l, m are lines, then their meet is denoted l m. The circle through points A, B and C (the circumcircle of ΔABC) is denoted ⊙ABC.
Given ΔABC, let the points Xi, Yi, Zi, lie on BC, CA, AB, respectively, for i = 1, 2, 3; that is, three distinct points on each side of the triangle, and suppose
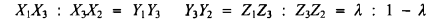
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012
References
2.
Bradley, C. J., Generalisation of the Droz-Famy lines, Math. Gaz.
92 (July 2008) pp. 332–335.Google Scholar
3.
Ehrmann, J.-P. and van Lamoen, F. M., A projective generalization of the Droz-Famy line theorem, Forum Geom.
4 (2004) pp. 225–227.Google Scholar
4.
Ayme, J.-L., A purely synthetic proof of the Droz-Famy Line theorem, Forum Geom.
4 (2004) pp. 219–224.Google Scholar
7.
Coxeter, H. S. M. and Greitzer, S. L., Geometry revisited, Random House/Singer (1967).CrossRefGoogle Scholar
8.
Bradley, C. J., Conjugation 2: Conjugate lines in a triangle, Math. Gaz.
93 (November 2009) pp. 420–432.CrossRefGoogle Scholar


