Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T15:18:18.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisibility properties for Fibonacci and related numbers

Published online by Cambridge University Press:  23 January 2015

Jawad Sadek  and
Russell Euler
Jawad Sadek
Affiliation:
Dept. of Mathematics and Statistics, NWMSU, Maryville, MO, 64468 USA e-mail: [email protected], [email protected]
Russell Euler
Affiliation:
Dept. of Mathematics and Statistics, NWMSU, Maryville, MO, 64468 USA e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Although it is an old one, the fascinating world of Fibonnaci numbers and Lucas numbers continues to provide rich areas of investigation for professional and amateur mathematicians. We revisit divisibility properties for t0hose numbers along with the closely related Pell numbers and Pell-Lucas numbers by providing a unified approach for our investigation.

For non-negative integers n, the recurrence relation defined by

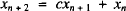
with initial conditions

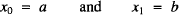
can be used to study the Pell (Pn), Fibonacci (Fn), Lucas (Ln), and Pell-Lucas (Qn) numbers in a unified way. In particular, if a = 0, b = 1 and c = 1, then (1) defines the Fibonacci numbers xn = Fn. If a = 2, b = 1 and c = 1, then xn = Ln. If a = 0, b = 1 and c = 2, then xn = Pn. If a =b = c = 2, then xn = Qn [1].

Type
Articles
Information
The Mathematical Gazette , Volume 97 , Issue 540 , November 2013 , pp. 461 - 464
Copyright
Copyright © The Mathematical Association 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Horadam, A. F. and Mahon, Bro. J. M., Pell and Pell-Lucas polynomials, The Fibonacci Quarterly, 23.1 (February 1985) pp. 7–20.Google Scholar
2. Koshy, T., Fibonacci and Lucas numbers with applications, Wiley, New York (2001).Google Scholar
3. Osler, T. J. and Hilbrun, A., An unusual proof that Fm divides Fmn using hyperbolic functions, Math. Gaz., 91 (November 2007) pp. 510–512.Google Scholar