Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T09:13:11.331Z Has data issue: false hasContentIssue false
  • English
  • Français

The Differentiation of a Function of a Function

Published online by Cambridge University Press:  03 November 2016

H. S. Carslaw
Get access Rights & Permissions [Opens in a new window]

Extract

If z is a function of y having a differential coefficient at a certain point, and y is a function of x having a differential coefficient at the corresponding point, then z is a function of x having a differential coefficient at that point, and this differential coefficient is given by the formula

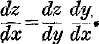
This theorem, thought not always stated so carefully, will be found in all texts on the calculus; but, so far as I am aware, no English writer, not even the most exact, offers a valid proof.

Type
Research Article
Information
The Mathematical Gazette , Volume 12 , Issue 170 , May 1924 , pp. 92 - 95
Copyright
Copyright © Mathematical Association 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page note 92 * A function is said to satisfy a certain condition in the neighbourhood of a point x=a, when there is a positive number h such that the condition is satisfied for all values of x from (a-h) to (a+h), i.e, when 0 < | x-a | ≦h, as a is usually excluded.