Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T08:14:55.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Deleting digits

Published online by Cambridge University Press:  03 February 2017

Ioulia N. Baoulina ,
Martin Kreh  and
Jörn Steuding
Ioulia N. Baoulina
Affiliation:
Department of Mathematics, Moscow State Pedagogical University, Krasnoprudnaya str. 14, Moscow 107140, Russia e-mail: [email protected]
Martin Kreh
Affiliation:
Department for Algebra and Number Theory, University of Hildesheim, Samelsonplatz 1, 31141 Hildesheim, Germany e-mail: [email protected]
Jörn Steuding
Affiliation:
Department of Mathematics, Würzburg University, Emil-Fischer-Str. 40, 97074 Würzburg, Germany e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We consider here the positive integers with respect to their unique decimal expansions, where each n ∈ ℕ is given by 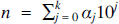for some non-negative integer k and digit sequence αkαk-1 … α0. With slight abuse of notation, we also use n to denote αkαk-1 … α0. For such sequences of digits (as well as for the numbers represented by the corresponding expansions) we write x ⊲ y if x is a subsequence of y, which means that either x = y or x can be obtained from y by deleting some digits of y. For example, 514 ⊲ 352148. The main problem is as follows: Given a set S ⊂ ℕ, find the smallest possible set M ⊂ S such that for all s ∈ S there exists m ∈ M with m ⊲ s.

Type
Articles
Information
The Mathematical Gazette , Volume 101 , Issue 550 , March 2017 , pp. 60 - 68
Copyright
Copyright © Mathematical Association 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Higman, G., Ordering by divisibility in abstract algebras, Proc. London Math. Soc. 2 (1952) pp. 326–336.CrossRefGoogle Scholar
2. Sakarovitch, J. and Simon, I., Subwords, in Combinatorics on Words, Lothaire, M. (ed.), Encyclopedia of Mathematics and its Applications, Vol. 17, Addison-Wesley (1983).Google Scholar
3. Shallit, J. O., Minimal primes, J. Recreational Math. 30 (2000) pp. 113–117.Google Scholar
4. Kreh, M., Minimal sets, J. Integer Seq. 18 (2015) Article 15.5.3.Google Scholar
5. Bright, C., Devillers, R. and Shallit, J., Minimal elements for the prime numbers, Exp. Math. 25 (2016) pp. 321–331.Google Scholar
6. Dickson, L. E., History of number theory. Vol. I, Carnegie Institution of Washington (1919).Google Scholar
7. Lucas, É., Sur les nombres parfaits, Mathesis 10 (1890) pp. 74–76.Google Scholar