Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-26T11:10:16.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugation 2: Conjugate lines in a triangle

Published online by Cambridge University Press:  01 August 2016

C. J. Bradley
C. J. Bradley*
Affiliation:
Flat 4, Terrill Court, 12–14 Apsley Court, Clifton, Bristol BS8 2SP
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous note the present author has given an account of the conjugations known as isogonal conjugation and isotomic conjugation with respect to a given triangle and has shown how to generalise the idea of conjugation involving a pair of points so that P(l, m, n) is q-conjugate, by means of a construction involving a transversal q, to the point 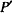(p2/l, q2/m, r2/n) and he has also demonstrated how to perform the geometrical constructions involved. When there is a self-conjugate point at the incentre I one has isogonal conjugation, and when there is a self-conjugate point at the centroid G one has isotomic conjugation.

Type
Articles
Information
The Mathematical Gazette , Volume 93 , Issue 528 , November 2009 , pp. 420 - 432
Copyright
Copyright © The Mathematical Association 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bradley, C.J., Conjugation 1, Math Gaz. 93 (July 2009) pp. 232–236.Google Scholar
2. Bradley, C. J., The algebra of geometry, Highperception (2007).Google Scholar
3. Droz-Farny, A., Question 14111 Educational Times, 71 (1899) pp. 89–90.Google Scholar
4. Ayme, J.-L., A purely synthetic proof of the Droz-Farny line theorem, Forum Geom., 4 (2004) pp. 219–224.Google Scholar
5. Thas, C., The Droz-Farny theorem and related topics, Forum Geom., 6 (2006) pp. 235–240.Google Scholar
6. Semple, J. G. and Kneebone, G. T., Algebraic projective geometry, Oxford (1952).Google Scholar
7. Bradley, C. J. and Smith, G. C., Triangle porisms with stationary centres, submitted for publication to Forum Geom.Google Scholar
8. Bradley, C. J., Monk, D. and Smith, G. C., On a porism associated with the Euler and Droz-Farny Lines, Forum Geom., 7 (2007) pp. 11–17.Google Scholar
9. Bradley, C. J., Generalisation of the Droz-Farny line, Math. Gaz., 92 (July 2008) pp. 332–335.10.1017/S0025557200183366CrossRefGoogle Scholar