Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T22:57:08.670Z Has data issue: false hasContentIssue false
  • English
  • Français

An alternative recursive formula for the sums of powers of integers

Published online by Cambridge University Press:  14 June 2016

José Luis Cereceda
José Luis Cereceda*
Affiliation:
Distrito Telefónica, Edificio Este 1, 28050 – Madrid, Spain e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The sums of powers of the first n positive integers Sp(n) = 1p + 2p + …+np, (p = 0, 1, 2, … )satisfy the fundamental identity

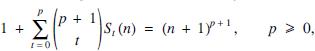(1)

from which we can successively compute S0 (n), S1 (n), S2 (n), etc. Identity (1) can easily be proved by using the binomial theorem; see e.g. [1, 2]. Several variations of (1) are also well known [3, 4, 5].

In this note, we derive the following lesser-known recursive formula for Sp (n):

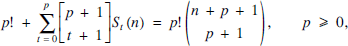(2)

where 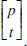denote the (unsigned) Stirling numbers of the first kind, also known as the Stirling cycle numbers (see e.g. [6, Chapter 6]). Table 1 shows the first few rows of the Stirling number triangle. Although the recursive formula (2) is by no means new, our purpose in dealing with recurrence (2) in this note is two-fold. On one hand, we aim to provide a new algebraic proof of (2) by making use of two related identities involving the harmonic numbers.

Type
Research Article
Information
The Mathematical Gazette , Volume 100 , Issue 548 , July 2016 , pp. 233 - 238
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Kelly, C., An algorithm for sums of integer powers, Math. Mag. 57 (1984) pp. 296–297.CrossRefGoogle Scholar
2.Owens, R. W., Sums of powers of integers, Math. Mag. 65 (1992) pp. 38–40.Google Scholar
3.Snow, D. R., Some identities for sums of powers of integers, Proceedings of Utah Academy of Sciences, Arts, and Letters, 52 Part 2 (1975) pp. 29–31.Google Scholar
4.Turner, B., Sums of powers of integers via the binomial theorem, Math. Mag. 53 (1980) pp. 92–96.Google Scholar
5.Acu, D., Some algorithms for the sums of integer powers, Math. Mag. 61 (1988) pp. 189–191.Google Scholar
6.DeTemple, D. and Webb, W., Combinatorial reasoning: an introduction to the art of counting (1st edn.) John Wiley (2014).Google Scholar
7.Chorlton, F., Summation by parts, Math. Spectrum 30 (1997/1998) p. 30.Google Scholar
8.Koshy, T., The ubiquitous Catalan numbers, Math. Teacher 100 (2006) pp. 184–188.CrossRefGoogle Scholar