Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T18:01:31.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic and geometric definitions of the cross product: the link

Published online by Cambridge University Press:  12 November 2024

François Dubeau
François Dubeau*
Affiliation:
Département de mathématiques, Faculté des sciences, Université de Sherbrooke 2500, boul. de l’Université, Sherbrooke (Qc), Canada, J1K 2R1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given two vectors 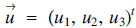$\overrightarrow u= {({u_1},\,\,{u_2},\,{u_3})^t}$ and 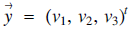$\overrightarrow y= {({v_1},\,{v_2},\,{v_3})^t}$ in 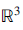${{\mathcal{R}}^3}$, the cross product 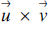$\overrightarrow u\times \overrightarrow v $is defined as follows (see [1] or [2]):

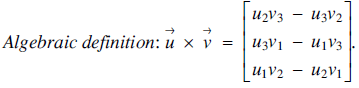$$Algebraic{\rm{ }}definition{\rm{:}}\,\,\overrightarrow u\times \overrightarrow v \, = \,\left[ {\matrix{ {{u_2}{v_3}} \hfill &-\hfill & {{u_3}{v_2}} \hfill\cr{{u_3}{v_1}} \hfill &-\hfill & {{u_1}{v_3}} \hfill\cr{{u_1}{v_2}} \hfill &-\hfill & {{u_2}{v_1}} \hfill\cr} } \right].$$

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 573 , November 2024 , pp. 470 - 477
Check for updates
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

References

Anton, H., Elementary linear algebra (8th edn.), Wiley (2000).Google Scholar
Strang, G., Introduction to linear algebra, (3rd edn.), Wellesley- Cambridge (2003).Google Scholar
Corral, M., Vector calculus, Springer (2008).Google Scholar
Hubbard, J. H. and Hubbard, B. B., Vector calculus, linear algebra, and differential forms (4th edn.), Matrix Editions (2009).Google Scholar
Colley, S. J., Vector calculus, (4th edn.), Pearson (2012).Google Scholar
Gao, F., A simple proof of the right-hand rule, Coll. Math. J. 44 (2013) pp. 227–229.CrossRefGoogle Scholar
Thurschwell, E., An even simpler proof of the right-hand rule, Coll. Math. J. 46 (2015) pp. 215–217.CrossRefGoogle Scholar
Hwang, S.-G. and Kim, I.-P. Orientation of the cross product in 3- vectors, Coll. Math. J. 50 (2019) pp. 298–299.CrossRefGoogle Scholar