Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T03:09:51.306Z Has data issue: false hasContentIssue false
  • English
  • Français

The Transformation y=f’(x)

Published online by Cambridge University Press:  03 November 2016

Raymond Garver
Get access Rights & Permissions [Opens in a new window]

Extract

The transformation y=f'(x) on the roots of

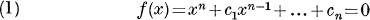
is intersting to study on account of the fact that it leads to a transformed equation whose constant term is, the discriminant of f(x)=0. It is easy to see that this property holds, for, writing f(x) in the factored form

Type
Research Article
Information
The Mathematical Gazette , Volume 17 , Issue 225 , October 1933 , pp. 251 - 256
Copyright
Copyright © Mathematical Association 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 251 note * In the American Mathematical Monthly, vol. 38 (1931), 185-6, I have used the transformation y = x2 to obtain the cubic discriminant, but in a different and less convenient way.

page 252 note * See School Science and Mathematics, vol. 29 (1929), 474-76, for a treatment based on essentially this transformation.

page 252 note † For details the reader may consult Dickson, First Course in the Theory of Equations, 1922, section 60.

page 254 note * See Dickson, Modem Algebraic Theories, 1926, 245; Kiepert, Journal für die reine und angewandte Mathematik, vol. 87 (1879), 132.

page 255 note * See, for example, Brioschi, Math. Annalen, vol. 13 (1878), 143-53.

page 255 note † yi (i = 1,2, ... 5) are the roots of the transformed equation.