No CrossRef data available.
Article contents
Sums of squares of integers in arithmetic progression
Published online by Cambridge University Press: 23 January 2015
Extract
The following striking identities
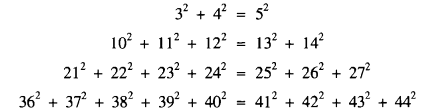
are the cases n = 1,2,3,4 of a remarkable family given by G.J. Dostor [1]:
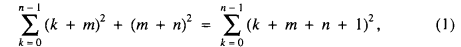
where m = n(2n + 1), and n = 1, 2, … The case m = −n is trivial. If m ≠ −n there are n + 1 squares of consecutive integers on the left and n on the right. We will treat the last term (m + n)2 on the left differently, and refer to it as a transition term relating two sums of squares of n consecutive integers.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012
References
1.
Dostor, G. J., Questions sur les nombres, Archiv der Mathematik und Physik, 64 (1879), pp. 350–352.Google Scholar
2.
Dickson, L. E., A history of the theory of numbers, Vol. II (Carnegie Institute, Washington, DC, 1920; reprinted Chelsea Pub., New York, NY, 1952; Dover Pub. Inc., New York, NY, 2005).Google Scholar


