Formulae are established below for

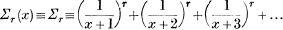
for both odd and even integer values of r(r>1), and x≥0; also for

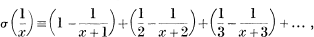
this series reducing to 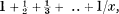when x is an integer

In 1920 I established the formula, a most useful one,

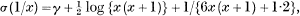
where γ is Euler’s constant

0·57721 56649 01532 86060 6,

and in 1920 gave a simpler proof with extension to higher powers of x(x + 1) with formulae for Σ2n+1, but not for Σ2n.