Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-22T05:19:43.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Some applications of the Chebyshev polynomials to polynomials in general

Published online by Cambridge University Press:  17 February 2025

G.J.O. Jameson
G.J.O. Jameson*
Affiliation:
13 Sandown Road, Lancaster LA1 4LN e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The Chebyshev polynomials: some basic facts

The Chebyshev polynomials Tn, named after the Russian mathematician P. L. Chebyshev (1821-1894), are defined by(1)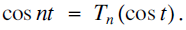

$${\text{cos }}nt = {T_n}({\text{cos }}t).$$

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 574 , March 2025 , pp. 93 - 100
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Rivlin, T. J., Chebyshev polynomials: from approximation theory to algebra and number theory (2nd edn.), Wiley (1990).Google Scholar
Cheney, E. W., Introduction to approximation theory, McGraw Hill (1966).Google Scholar
Jameson, G. J. O., Counting zeros of generalised polynomials: Descartes’ rule of signs and Laguerre’s extensions, Math. Gaz. 80 (July 2006) pp. 223–234.CrossRefGoogle Scholar
Jameson, G. J. O., The maximun modulus of a complex polynomial on the unit circle, Math. Gaz. 109 (March 2025) pp. 119.Google Scholar