Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T19:22:00.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Some alternative derivations of Craig's formula

Published online by Cambridge University Press:  15 June 2017

Seán M. Stewart
Seán M. Stewart*
Affiliation:
9 Tanang Street, Bomaderry NSW 2541, Australia e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In the performance of digital communication systems over fading channels, the error analysis is typically modelled using a Gaussian probability distribution. One function central to the analysis is what engineers routinely refer to as the (Gaussian) Q-function and is defined by

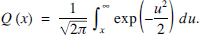1

This is the canonical representation used for the function. In this paper a number of derivations of an important alternative representation for the Q-function known as Craig's formula will be given.

Type
Articles
Information
The Mathematical Gazette , Volume 101 , Issue 551 , July 2017 , pp. 268 - 279
Copyright
Copyright © Mathematical Association 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Craig, J. W., A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations, in IEEE MILCOM'91 Conf. Rec., Boston, MA (1991) pp. 25.2.1–25.5.5. Google Scholar
2. Lebedev, N. N., Special functions and their applications, Dover Publications (1972).Google Scholar
3. Weinstein, F. S., Simplified relationships for the probability distribution of the phase of a sine wave in narrow-band normal noise, IEEE Trans. Inf. Theory, 20 (1974) pp. 658–661.Google Scholar
4. Pawula, R. F., Rice, S. O., and Roberts, J. H., Distribution of the phase angle between two vectors perturbed by Gaussian noise, IEEE Trans. Commun. 30 (1982) pp. 1828–1841.Google Scholar
5. Iwasawa, H., Gaussian integral puzzle, Math. Intell. 31 (2009) pp. 38–41.CrossRefGoogle Scholar
6. Simon, M. K. and Alouini, M.-S., Digital communication over fading channels (2nd edn.), Wiley (2005).Google Scholar
7. Savischenko, N. V., Special integral functions used in wireless communications theory, World Scientific Publishing Company (2014).Google Scholar
8. Ng, E. W. and Geller, M., A table of integrals of the error functions, J. Res. Nat. Bur. Stand., Sec. B 73B (1969) pp. 1–20.CrossRefGoogle Scholar
9. Abramowitz, M. and Stegun, I. A. (eds.), Handbook of mathematical functions with formulas, graphs, and mathematical tables, Dover Publications (1972).Google Scholar
10. Simon, M. K., Some new twists to problems involving the Gaussian probability integral IEEE Trans. Commun. 46 (1998) pp. 200–210.Google Scholar
11. Lever, K. V., New derivation of Craig's formula for the Gaussian probability function, Electron. Lett. 34 (1998) pp. 1821–1822.Google Scholar
12. Tellambura, C. and Annamalai, A., Derivation of Craig's formula for Gaussian probability function, Electron. Lett. 35 (1999) pp. 1424–1425.Google Scholar