Article contents
Smooth curves of constant width
Published online by Cambridge University Press: 22 September 2016
Extract
The construction of curves of constant width using circular arcs is well known; the procedure may be found, for example, in [1]. This article describes a different method for constructing a family of ‘smooth’ curves of constant width. Basic properties of such curves may be found in [1].
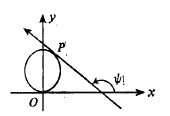
Let C be a regular, smooth, and convex curve in the euclidean plane. Regularity implies that each point of C lies on only one support line and each support line contains only one point of C, smoothness implies the existence of derivatives at each point of C, and convexity implies the curve is a simple closed curve whose interior points form a convex set. Select a point O on C as origin, use the support line to C at O as the x-axis, and give the curve a counter-clockwise orientation (see Fig. 1).
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1976
References
- 6
- Cited by


