The following method of introducing the ideas of rotation and strain into the study of Elasticity depends upon the identity

m · n grad u=n · (m grad u + m × curl u).....(1)

and upon the fact that if the straight line PQ undergoes a small rotation ω about an axis through P, the displacement of Q is

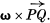
Consider first of all a rigid body which undergoes a small displacement. Let the point P of the body move to P′. We shall represent PP′ by u and regard u as typical of a vector field extending throughout the space originally occupied by the body. Let Q be a point near to P and represent 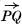by m.