Are there solutions of the equation x2 + 1 = 0 ? Carl Fredrich Gauss (1777–1855) conjectured that there was a solution and that it was the square root of - 1 . But since the squares of all real numbers, positive or negative, are positive, Gauss introduced a fanciful idea. His solution to this equation was 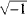, which he named i. He integrated i with the real numbers to form a set known as 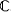, the complex numbers, where each element in that set was of the form a + bi, where a, 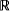. Gauss illustrated this on a graph, the horizontal axis became the real axis and represented the real coefficient, while the vertical axis became the imaginary axis and represented the imaginary coefficient.