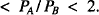No CrossRef data available.
Published online by Cambridge University Press: 01 August 2016
Let p1, p2, p3, … be the sequence of primes. Take any integer n ⩾ 2 and partition the set {p1p2, … , pn} into two non-empty subsets A and B. Let PA be the product of primes in A and PB be the product of primes in B. No partition exists with PA = PB, because of the uniqueness of prime factorisation, but Fernando Castro’s neat result in [1] asserts that for each n there is a partition for which 1