Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T03:30:14.894Z Has data issue: false hasContentIssue false
  • English
  • Français

On a simple set of integers

Published online by Cambridge University Press:  01 August 2016

Juan Pla
Juan Pla*
Affiliation:
315 rue de Belleville, 75019 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

During an investigation on some Diophantine systems, we were led to consider the following set

where x, y, a, b, c are indeterminate integers.

From elementary algebra we know that, if they exist, x and y are the roots of the quadratic equation

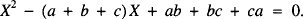
Type
Articles
Information
The Mathematical Gazette , Volume 93 , Issue 527 , July 2009 , pp. 200 - 212
Copyright
Copyright © The Mathematical Association 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Lucas, Edouard, Théorie des nombres, Gauthier-Villars, Paris (1891), p. 128, Exemple V (as reprinted by Jacques Gabay, Paris, 1991).Google Scholar
2. Berndt, Bruce, Ramanujan notebooks, Part IV, Springer Verlag, New York (1994).Google Scholar
3. Dickson, Leonard E., History of the theory of numbers, Carnegie Institution of Washington, Washington (1920) 2, pp. 705–711.Google Scholar
4. Bini, U., Sur quelques questions d’analyse indéterminée, Mathesis, 3ème série, 9, (1909) pp. 113–118.Google Scholar
5. Tito Piezas III: Ramanujan 6-10-8 identity at http:// mathworld.wolfram.com/Ramanujan6-10-8Identity.html Google Scholar
6. Tito Piezas III: Hirschhorn 3-5-7 identity at http:// mathworld.wolfram.com/Hirschhorn3-7-5Identity.html Google Scholar
7. Hirschhorn, M.D., Two or three identities of Ramanujan, Amer. Math. Monthly, 105-1 (1998) pp. 52–55.Google Scholar
8. Martin, Artemas, A rigorous method for finding biquadrate numbers whose sum is biquadrate, Deuxième Congrès International des Mathématiciens, Paris, 1900, pp. 239–248.Google Scholar
9. Euler, L., Solutio generalis quorundam problematum Diophanteorum, quae vulgo nonnisi solutiones speciales admitiere videntur, Opera Omnia, Series 1, Volume 2, pp. 428–458.Google Scholar
10. Hoggatt, V.E., Fibonacci and Lucas numbers, Houghton Mifflin (1969).Google Scholar
11. Euler, L., Supplementum quorundam theorematum Arithmeticorum quae in nonnullis demonstrationibus supponuntur, Opera Omnia, Series 1, Volume 2, pp. 556–575.Google Scholar