Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T15:30:47.342Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Problem in Elementary Geometry

Published online by Cambridge University Press:  03 November 2016

F G. Maunsell  and
D. Pedoe
Get access Rights & Permissions [Opens in a new window]

Extract

The rectangle ABCD is supposed to lie in a vertical plane, with AB horizontal. P is any point in the horizontal plane through CD. Prove that ∠APB < ∠CPD.

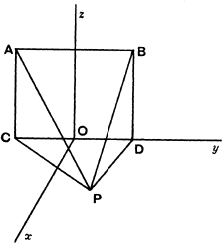
Provided that the perpendicular from P on to CD meets CD between C and D, this theorem is true and easily proved by comparing the angles into which a plane through P perpendicular to the rectangle divides the two angles considered. The sine of each of the angles into which ∠APB is divided is less than the sine of the corresponding angle in ∠CPD.

Type
Research Article
Information
The Mathematical Gazette , Volume 25 , Issue 265 , July 1941 , pp. 136 - 140
Copyright
Copyright © Mathematical Association 1941 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)