Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T08:53:08.475Z Has data issue: false hasContentIssue false
  • English
  • Français

A novel method to solve the quartic equation

Published online by Cambridge University Press:  12 October 2022

Abdel Missa  and
Chrif Youssfi
Abdel Missa
Affiliation:
Department of Finance, Jacksonville University, 2800 University Blvd N, Jacksonville FL 32211 USA e-mail: [email protected]
Chrif Youssfi
Affiliation:
MarketCipher Partners, Quantitative Research, Rabat, Morocco e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The first solution to the quartic equation is attributed to Lodovico Ferrari, a student of Geralamo Cardano. The solution was published alongside the solution of the cubic in Cardano’s book Ars Magna [1]. In this Article, we introduce a new canonical form to simplify the derivation of the roots of the equation (1)

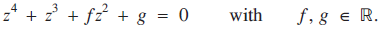$${z^4} + {z^3} + f{z^2} + g = 0\quad \textrm{with}\quad f,g \in \mathbb{R}.$$

Type
Articles
Information
The Mathematical Gazette , Volume 106 , Issue 567 , November 2022 , pp. 480 - 486
Check for updates
Copyright
© The Authors, 2022. Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cardano, Girolamo, Ars Magna (1545).Google Scholar