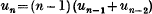One of the best known of all classical elementary combinatorial problems is the enumeration of the derangements of n letters A1 A2,…, An, i.e., the permutations of these letters in a row so that, for every i, At is not the ¿th letter. The question is frequently presented in the form of an office boy who puts n differently addressed letters into n envelopes; we then seek the number of ways (w„) in which he can send every letter to a wrong address. Textbooks almost invariably solve the problem by deducing from general reasoning the recurrence relation :