Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T12:09:55.675Z Has data issue: false hasContentIssue false
  • English
  • Français

The most elementary proof that ?

Published online by Cambridge University Press:  17 October 2016

Nick Lord
Nick Lord*
Affiliation:
Tonbridge School, Kent TN9 1JP
Get access Rights & Permissions [Opens in a new window]

Extract

Here we present a simplification of one of the standard proofs that . We then look at extensions of the new approach, and add comments on the nature of the simplification (which relates to Step 1 below) and finally on the literature.

As in most proofs of the result, we shall actually prove that ; because

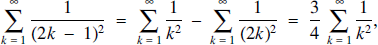
this is equivalent to the result sought.

Type
Articles
Information
The Mathematical Gazette , Volume 100 , Issue 549 , November 2016 , pp. 429 - 434
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Durell, C. V. & Robson, A., Advanced trigonometry, G. Bell & Sons (1930).Google Scholar
2. Yaglom, A. M. & Yaglom, I. M., An elementary derivation of the formulas of Wallis, Leibniz and Euler for the number π, Uspekhi Mat. Nauk. 57 (1953) pp.181–187 [also available at http://www.mathnet.ru ]Google Scholar
3. Yaglom, A. M. & Yaglom, I. M., Challenging mathematical problems with elementary solutions, Volume 2, Dover (2003), Problem 145.Google Scholar
4. Papadimitriou, I., A simple proof of the formula , Amer. Math. Monthly 80 (1973) pp. 424–425.Google Scholar
5. Apostol, T. M., Mathematical analysis (2nd edn.), Addison-Wesley (1974) p. 30, pp. 216-217.Google Scholar
6. Chapman, R., Evaluating ζ (2), accessed June 2016 at http://empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf Google Scholar
7. Bromwich, T. J. I'A., An introduction to the theory of infinite series (2nd edn.), Macmillan (1959).Google Scholar
8. Berndt, B. C. & Yeap, B. P., Explicit evaluations and reciprocity theorems for finite trigonometric sums, Advances in Applied Math. 29 (2002) pp. 358–385.CrossRefGoogle Scholar
9. Stark, E. L., The series , once more, Math. Mag. 47 (1974) pp. 197–202.Google Scholar
10. Cauchy, A-L., Cours d'analyse de l'École Royale Polytechnique (Volume 1) (1821), pp. 556–559: available in many printings such as the Cambridge Library Collection, Cambridge University Press (2009).CrossRefGoogle Scholar
11. Apostol, T. M., Another elementary proof of Euler's formula for ζ (2n), Amer. Math. Monthly 80 (1973) pp. 425–431.Google Scholar