Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-21T18:22:31.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Linearly periodic continued fractions

Published online by Cambridge University Press:  13 October 2021

Kantaphon Kuhapatanakul  and
Lalitphat Sukruan
Kantaphon Kuhapatanakul
Affiliation:
Department of Mathematics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand, e-mail: [email protected]
Lalitphat Sukruan
Affiliation:
Department of Mathematics, Faculty of Science and Technology, Rajamangala University of Technology Suvarnabhumi, Suphanburi, Thailand, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

An infinite simple continued fraction representation of a real number α is in the form

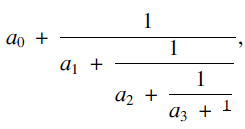$$\eqalign{& {a_0} + {1 \over {{a_1} + {1 \over {{a_2} + {1 \over {{a_3} + {1 \over {}}}}}}}} \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \cr} $$
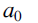where $${a_0}$$ is an integer, and 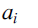$${a_i}$$ are positive integers for 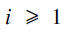$$i \ge 1$$. This is often written more compactly in one of the following ways:
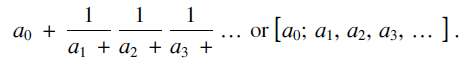$${a_0} + {1 \over {{a_1} + }}{1 \over {{a_2} + }}{1 \over {{a_3} + }} \ldots \;{\rm{or}}\;\left[ {{a_0};\;{a_1},\;{a_2},\;{a_3} \ldots } \right]$$
.

Type
Articles
Information
The Mathematical Gazette , Volume 105 , Issue 564 , November 2021 , pp. 442 - 449
Check for updates
Copyright
© The Mathematical Association 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cohn, H., A short proof of the simple continued fraction expansion of e, Amer. Math. Monthly 113(1) (2006) pp. 57-62.Google Scholar
Komatsu, T., Hurwitz and Tasoev continued fractions, Monatsh. Math. 145 (2005) pp. 47-60.CrossRefGoogle Scholar
Osler, T. J., A proof of the continued fraction expansion of , Amer. Math. Monthly 113(1) (2006) pp. 62-66.Google Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of number, Oxford University Press (4th edn.) (1960).Google Scholar
Jones, W. B. and Thron, W. J., Continued fractions: analytic theory and applications, Encyclopedia of mathematics and its applications Vol.11, Addison-Wesley Publishing Company (1980).Google Scholar
Laohakosol, V. and Kuhapatanakul, K., The reverse irrationality criteria of Brun and Badea, East-West J. Math., Special volume (2008) pp. 217-234.Google Scholar