Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T07:21:19.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear differential equations with constant coefficients

Published online by Cambridge University Press:  06 June 2019

Bethany Fralick  and
Reginald Koo
Bethany Fralick
Affiliation:
Department of Mathematical Sciences, University of South Carolina Aiken, USA
Reginald Koo
Affiliation:
Department of Mathematical Sciences, University of South Carolina Aiken, USA
Get access Rights & Permissions [Opens in a new window]

Extract

We consider the second order homogeneous linear differential equation (H)

$${ ay'' + by' + cy = 0 }$$
with real coefficients a, b, c, and a ≠ 0. The function y = emx is a solution if, and only if, m satisfies the auxiliary equation am2 + bm + c = 0. When the roots of this are the complex conjugates m = p ± iq, then y = e(p ± iq)x are complex solutions of (H). Nevertheless, real solutions are given by y = c1epx cos qx + c2epx sin qx.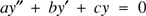

Type
Articles
Information
The Mathematical Gazette , Volume 103 , Issue 557 , July 2019 , pp. 257 - 264
Copyright
© Mathematical Association 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Plumpton, C. and Tomkys, W. A.: Sixth form pure mathematics, Volume two, Pergamon Press (1963).Google Scholar