Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T08:18:29.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Differential Equations and the Oscillatory Property of Maclaurin's Cosine Series

Published online by Cambridge University Press:  03 November 2016

Aurel Wintner
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that, if.

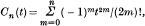
cos t>Cn(t) or cos t<Cn(t) holds for 0< t< ∞ according as n = 1, 3, 5, … or n = 2, 4, 6, …. It will be noted that this is not obvious in itself. In fact, the absolute values of the successive terms of the alternating series 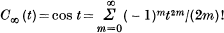do not decrease from m = 0 onward, except when t is small.

Type
Research Article
Information
The Mathematical Gazette , Volume 33 , Issue 303 , February 1949 , pp. 26 - 28
Copyright
Copyright © The Mathematical Association 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)