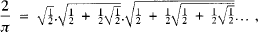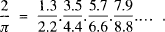Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Osler, T. J.
2007.
A simple geometric method of estimating the error in using Vieta's product forπ.
International Journal of Mathematical Education in Science and Technology,
Vol. 38,
Issue. 1,
p.
136.