Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T18:28:04.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional Calculus

Published online by Cambridge University Press:  03 November 2016

W Fabian
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper we considered fractional integration and differentiation of functions of a real variable. In the present paper the complex variable will be used.

We define a λth integral, or a (−λ)th differential coefficient, of f(z) along a simple curve l by

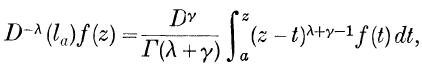
where the integration and differentiation are along l, starting from a, λ is any number, real or complex, γ is the least integer greater than or equal to zero such that R(λ) + γ > 0, R(λ) being the real part of λ; and D stands for 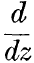, denoting differentiation along l. a is arbitrary and independent of z, and in the present paper is to be taken as finite.

Type
Research Article
Information
The Mathematical Gazette , Volume 20 , Issue 240 , October 1936 , pp. 249 - 253
Copyright
Copyright © Mathematical Association 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page no 249 note * Fabian, , Math. Gazette (1936), vol. xx, no. 1, pp. 88–92 CrossRefGoogle Scholar.

page no 249 note † Fabian, , Phil. Mag., ser. 7, vol. xx, pp. 781-78 (1935)CrossRefGoogle Scholar.

page no 251 note * Fabian, , Phil. Mag. (1936), ser. 7, vol. xxi, pp. 274–280 CrossRefGoogle Scholar.

page no 251 note † If f(z) has M cycles at p, f(z) is to be regarded as having M branch-points at p, and the theorem applies to each of the M branch-points at p separately.

page no 251 note ‡ Fabian, Phil. Mag. (1936).