Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T14:55:06.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional Calculus

Published online by Cambridge University Press:  03 November 2016

W. Fabian
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let f(x) be a real function of a real variable x. The meanings of 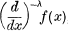when λ is a positive integer, a negative integer and zero, are well known. In the first case, 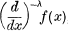denotes the λth integral of f(x) with respect to x, with an arbitrary lower limit of integration. In the second case, 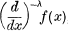stands for the (−λ)th differential coefficient of f(x) with respect to x. Lastly, when λ = 0, 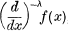means f(x).

Type
Research Article
Information
The Mathematical Gazette , Volume 20 , Issue 238 , May 1936 , pp. 88 - 92
Copyright
Copyright © Mathematical Association 1936 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Page no 88 note * Leibnitz, Opera, ed. Dutens, 3, Commercium Phiols. et Math., p. 105(1695).

Page no 88 note † Liouville, , Journal de l’Ecole Polytechnic, 13, pp.1–186 (1832)Google Scholar.

Page no 88 note ‡ Riemann, Gesammelte Werke, pp. 331-344 (1876).

Page no 88 note § Ferrar, , Proc. Edin. Math. Soc., 48, pp. 92–105 (1927).CrossRefGoogle Scholar

Page no 89 note * Fabian, , Philosophical Magazine, ser. 7, vol. 20, pp. 781–789 (1935)Google Scholar. The index laws and the Riemann series are dealt with here.