Article contents
Finding sums of powers using physical arguments
Published online by Cambridge University Press: 15 June 2017
Extract
In an earlier issue of the Mathematical Gazette, Nick Lord established the familiar formula for the sum of the first n squares using a physical argument based on the centroid of a configuration of masses in the plane [1]. In [2] we demonstrate an alternative configuration that gives the same result. This article is a follow-up to these papers, in which we find physical derivations of the formula for
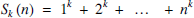
for each k ∈ {1, 2, 3, 4, 5}. Let us first summarise the required theory. Take any region X ⊆ ℝ2 with uniform density and total area A. The centroid of is the arithmetic mean position of all of the points in X. If a region has a line of symmetry then the centroid will be located on that line.
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2017
References
- 3
- Cited by


