No CrossRef data available.
Article contents
Fibonacci-Lucas hyperbolas
Published online by Cambridge University Press: 22 June 2022
Extract
Let us define a Fibonacci-Lucas hyperbola as a hyperbola passing through an infinite number of points of the form (Fm, Ln), where the Fm are distinct Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21,…, where F0 = 0), and the Ln are distinct Lucas numbers (2, 1, 3, 4, 7, 11, 18, 29,…,. where L0 = 2). The simplest examples are 5x2 - y2 = 4, which contains the points (Fk, Lk) with odd subscripts, e.g. (1, 1), (2, 4), (5, 11), and 5x2 - y2 = -4, which contains the points with even subscripts, e.g. (0, 2), (1, 3), (3, 7); (see [1, 2]). These follow immediately from the identity
(1)
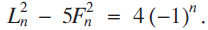 $$L_n^2 - 5F_n^2 = 4{( - 1)^n}.$$
$$L_n^2 - 5F_n^2 = 4{( - 1)^n}.$$
- Type
- Articles
- Information
- Copyright
- © The Authors, 2022 Published by Cambridge University Press on behalf of The Mathematical Association



