Published online by Cambridge University Press: 01 August 2016
Cyclotomic polynomials, (xp - l)/(x-1), have (p-1) zeros exp(2πiq/p) (q = 1, 2, ... ,p - 1). We consider related polynomials whose zeros are given by cos(qπ/p) (q = 1, 2, ... ,p - 1) and indicate their relation to polynomials Pn (ζ) that satisfy the ‘double angle’ condition Pn(2ζ2 - l) = Pn(ζ)Pn(-ζ). The double angle condition is generalised to a chain of double angle conditions Qi(2ζ2 - 1) = Qi+1(ζ)Qi+1(-ζ), i = 1, 2, ...,n(Q1 ≡ Qn+1) For purposes of illustration, we will focus on P4(ζ), demonstrating how construction of the fourth order polynomial subject to the double angle condition yields an equation for cos 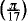 . We also discuss more general features of the polynomials Pn (ζ). Furthermore, we illustrate how a simple geometrical construction can be used to derive a polynomial for cos
. We also discuss more general features of the polynomials Pn (ζ). Furthermore, we illustrate how a simple geometrical construction can be used to derive a polynomial for cos 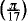 .
.