Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T01:28:38.825Z Has data issue: false hasContentIssue false
  • English
  • Français

A dual to a BMO Problem

Published online by Cambridge University Press:  01 August 2016

Michael de Villiers
Get access Rights & Permissions [Opens in a new window]

Abstract

An abstract is not available for this content so a preview has been provided. Please use the Get access link above for information on how to access this content.
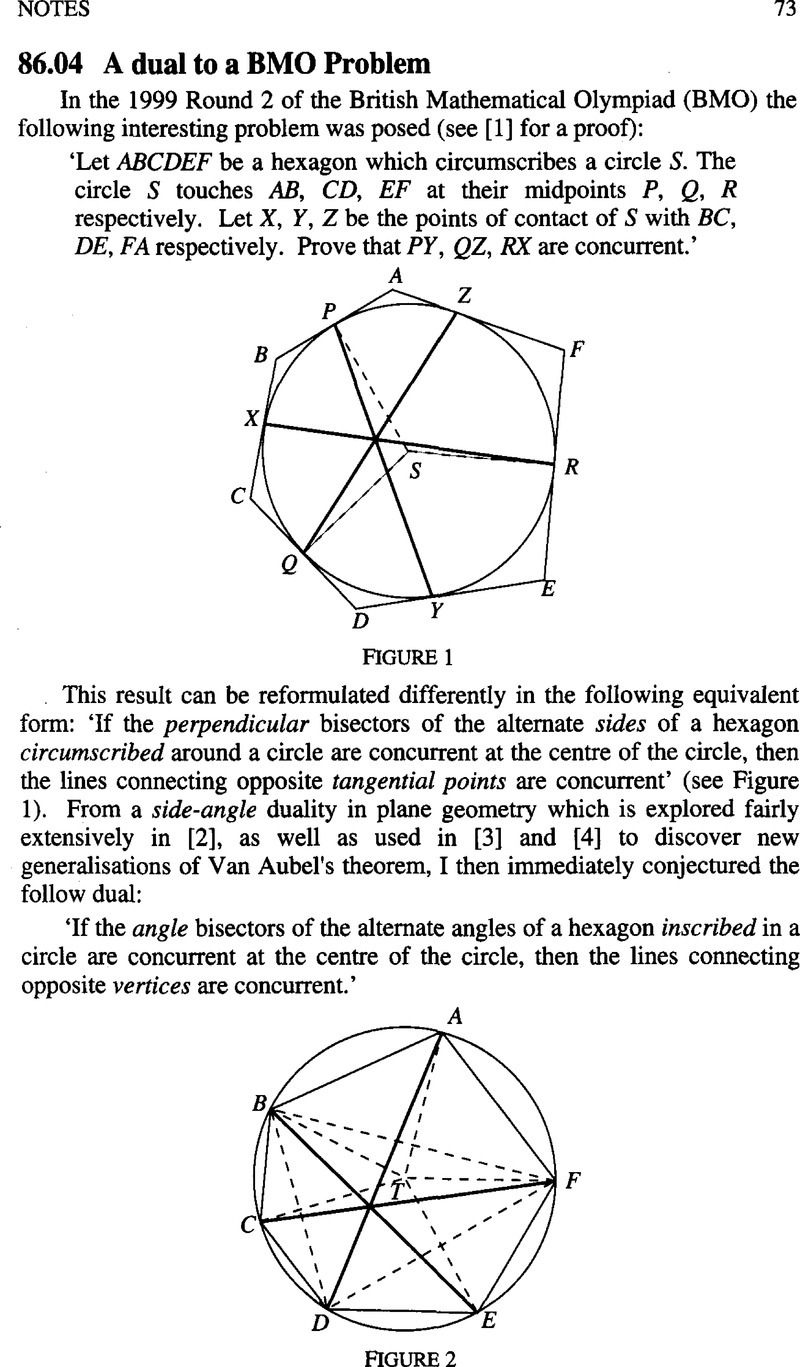
Image of the first page of this content. For PDF version, please use the ‘Save PDF’ preceeding this image.'
Type
Notes
Information
The Mathematical Gazette , Volume 86 , Issue 505 , March 2002 , pp. 73 - 74
Copyright
Copyright © The Mathematical Association 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. The UK Mathematics Trust Yearbook 1998–1999, pp. 92–94.Google Scholar
2. de Villiers, M. Some adventures in Euclidean geometry. University of Durban-Westville: Durban, South Africa, 1996.Google Scholar
3. de Villiers, M. Dual generalisations of Van Aubel’s theorem, Math. Gaz. 82 (November 1998) pp. 405–412.Google Scholar
4. de Villiers, M. More on dual Van Aubel generalisations, Math. Gaz. 84 (March 2000) pp. 121–122.CrossRefGoogle Scholar