Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T01:25:56.708Z Has data issue: false hasContentIssue false
  • English
  • Français

A cubic surface of revolution

Published online by Cambridge University Press:  23 January 2015

Mark B. Villarino
Mark B. Villarino*
Affiliation:
Escuela de Matemática, Universidad de Costa Rica, 11501 San José, Costa Rica
Get access Rights & Permissions [Opens in a new window]

Extract

A well-known exercise in classical differential geometry [1, 2, 3] is to show that the set 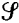of all points (x, y, z) ∈ ℝ3 which satisfy the cubic equation

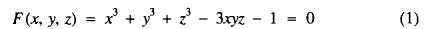
is a surface of revolution.

The standard proof ([2], [3, p. 11]), which, in principle, goes back to Lagrange [4] and Monge [5], is to verify that (1) satisfies the partial differential equation (here written as a determinant)

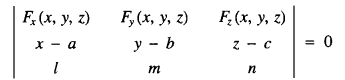
which characterises any surface of revolution F (x, y, z) = 0 whose axis of revolution has direction numbers (l, m, n) and goes through the point (a, b, c). This PDE, for its part, expresses the geometric property that the normal line through any point of 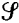must intersect the axis of revolution (this is rather subtle; see [6]). All of this, though perfectly correct, seems complicated and rather sophisticated just to show that one can obtain 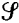by rotating a suitable curve around a certain fixed line. Moreover, to carry out this proof one needs to know a priori just what this axis is, something not immediately clear from the statement of the problem. Nor does the solution give much of a clue as to which curve one rotates.

A search of the literature failed to turn up a treatment of the problem which differs significantly from that sketched above (although see [1]).

The polynomial (1) is quite famous and has been the object of numerous algebraical and number theoretical investigations. See the delightful and informative paper [7].

Type
Articles
Information
The Mathematical Gazette , Volume 98 , Issue 542 , July 2014 , pp. 281 - 290
Copyright
Copyright © Mathematical Association 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barani, Jean-Pierre, Courbes et surfaces (2008), p. 27, available at http://jean-pierre.barani.pagesperso-orange.fr/Courbes et surfaces.pdf Google Scholar
2. Dean, George R., Solution to Problem 365, Annals of Mathematics 8 (1893-1894), p. 163, also available at http://www.jstor.orglstable/1967952 Google Scholar
3. Salmon, George, Treatise on the analytic geometry of three dimensions, Vol. 2, Longmans, Green and Co. (1915).Google Scholar
4. Lagrange, Joseph-Louis, Sur différentes questions d'analyse relatives a la théorie des intégrales particuliéres, Nouveaux mémoires de l'Academie Royale des Sciences et Belles-Lettres de Berlin (1779); Oeuvres Completes 4, pp. 585–634.Google Scholar
5. Monge, Gaspard, Feuilles d'analyse appliquée à la géométrie, 1795; reprint edition, Jacques Gabay, Paris (2008).Google Scholar
6. Gleason, Andrew M., Greenwood, R. E. and Kelly, Leon M., William Lowell Putnam Mathematical Competition: problems and solutions: 1938-1964, Mathematical Association of America (2003) pp. 433–436.Google Scholar
7. MacHale, Des, My favourite polynomial, Math. Gaz. 75 (June 1991) pp. 157–165.Google Scholar
8. Wikipedia, Cubic surface, accessed on 26 February 2014 at http://en.wikipedia.orglwiki/Cubic surface Google Scholar
9. Polo-Blanco, Irene and Top, Jaap, Explicit real cubic surfaces, Canad. Math. Bull. 51 (2008) pp. 125–133.Google Scholar
10. Hilbert, D., Geometry and the imagination, Chelsea, New York (1952), also available at http://math.stackexchange.com/questions/222667 Google Scholar
11. Henderson, Archibald, The twenty-seven lines on the cubic surface, Cambridge University Press (1911).Google Scholar
12. Schläfli, Ludwig, On the distribution of surfaces of the third order into species in reference to the absence or presence of singular points, and the reality of their lines, Philosophical Transactions of the Royal Society of London, 153 (1863) pp. 193–241.Google Scholar
13. Cayley, Arthur, A memoire on cubic surfaces, Philosophical Transactions of the Royal Society of London, 159 (1869) pp. 231–326.Google Scholar
14. Bruce, J. W. and Wall, C. T. C., On the classification of cubic surfaces, J. London Math. Soc. (2), 19 (1979) pp. 245–256.Google Scholar
15. Dickson, L. E., The history of the theory of numbers, Vol 2, Chelsea, New York (1963).Google Scholar
16. Mordell, L. J., Diophantine equations, Academic Press, New York (1969).Google Scholar
17. Chamberland, Marc, A natural extension of the Pythagorean equation to higher dimensions, Ramanujan Journal 16 (2008) pp. 169–179.Google Scholar