Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T09:17:53.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed form expressions for two harmonic continued fractions

Published online by Cambridge University Press:  16 October 2017

Martin Bunder  and
Joseph Tonien
Martin Bunder
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Australia e-mail: [email protected]
Joseph Tonien
Affiliation:
Institute of Cybersecurity and Cryptology, School of Computing and Information Technology, University of Wollongong, Australia e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

A continued fraction is an expression of the form

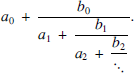
The expression can continue for ever, in which case it is called an infinite continued fraction, or it can stop after some term, when we call it a finite continued fraction. For irrational numbers, a continued fraction expansion often reveals beautiful number patterns which remain obscured in their decimal expansion. The interested reader is referred to [1] for a collection of many interesting continued fractions for famous mathematical constants.

Type
Articles
Information
The Mathematical Gazette , Volume 101 , Issue 552 , November 2017 , pp. 439 - 448
Copyright
Copyright © Mathematical Association 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Olds, C. D., Continued fractions, The Mathematical Association of America (1963).CrossRefGoogle Scholar
2. Wiener, M., Cryptanalysis of short RSA secret exponents, IEEE Transactions on Information Theory 36 (1990) pp. 553–558.CrossRefGoogle Scholar
3. Bunder, M. and Tonien, J., A new improved attack on RSA, Proceedings of the 5th International Cryptology and Information Security Conference (2016) pp. 101–110.Google Scholar
4. Seidel, L., Untersuchungen über die Konvergenz und Divergenz der Kettenbrüche, Habilschrift München (1846).Google Scholar
5. Stern, M. A., Über die Kennzeichen der Konvergenz eines Kettenbruchs, Journal für die Reine und Angewandte Mathematik 37 (1848) pp. 255–272.Google Scholar
6. Lorentzen, L. and Waadeland, H., Continued fractions, Volume 1, Convergence theory, Atlantis Press (2008).CrossRefGoogle Scholar
7. Beardon, A. F. and Short, I., The Seidel, Stern, Stolz and Van Vleck theorems on continued fractions, Bulletin of the London Mathematical Society 42(3) (2010) pp. 457–466.CrossRefGoogle Scholar
8. Euler, L., De fractionibus continuis observationes, Commentarii Academiae Scientiarum Imperialis Petropolitanae 11 (1750) pp. 32–81.Google Scholar
9. Frame, J. S., An approximation to the quotient of gamma function, The American Mathematical Monthly 56(8) (1949) pp. 529–535.Google Scholar
10. Tricomi, F. G. and Erdélyi, A., The asymptotic expansion of a ratio of gamma functions, Pacific Journal of Mathematics 1(1) (1951) pp. 133–142.CrossRefGoogle Scholar
11. Abramowitz, M. and Stegun, I., Handbook of mathematical functions with formulas, graphs, and mathematical tables, National Bureau of Standards (1964).Google Scholar