Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-22T05:33:20.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on sums of cubes

Published online by Cambridge University Press:  17 February 2025

A. F. Beardon
A. F. Beardon*
Affiliation:
DPMMS, University of Cambridge, CB3 0WB e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Here we are interested in the familiar identity 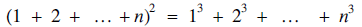but only in as far as it provides the solution (1, 2, …, n) of the Diophantine equation (1) 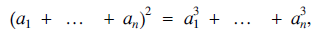where n and the aj are positive integers. In fact, not only is (1, 2, …, n) a solution of (1), it has the remarkable property that, up to a permutation of its entries, it is the only solution of (1) in which the aj are distinct (see Section 4). Thus any other solution will necessarily contain repetitions among the aj and, for this reason, a solution must be defined to be a sequence (which allows repetitions) rather than a set. However, we shall not distinguish between two solutions whose entries are permutations of each other.

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 574 , March 2025 , pp. 39 - 46
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbeau, E. and Seraj, S., Sum of cubes is square of sum, Notes on Number Theory and Discrete Mathematics, 19(1) pp. 1–13, available at https://nndtm.net/papers/nntdm-19/NNTDM−19−1−01−13.pdf Google Scholar
Liouville, J., Jour. de Mathématiques 2(2), Comptes Rendus, (1857) pp. 425-432.Google Scholar
Dickson, L., History of the theory of numbers, Vol. 1, Chelsea [1910] (republished 1971).Google Scholar
Pagni, D., An interesting number fact, Math. Gaz. 82 (July 1998) pp. 271-273.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (5th edn) Clarendon Press (1979).Google Scholar
Mason, J. H., Generalising ‘Sums of cubes equal to squares of sums’, Math. Gaz. 85 (March 2001) pp. 50-58.CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities, Cambridge (1978).Google Scholar
Bollobas, B., Linear Analysis, Cambridge (1990).Google Scholar
Beardon, A. F., Sums of powers of integers, Amer. Math. Monthly 103 (1996) pp. 201–213.Google Scholar