No CrossRef data available.
Article contents
Blocks of decimal digits
Published online by Cambridge University Press: 18 June 2018
Extract
Recently a friend kindly made me a birthday card whose background consisted of rows and rows of digits, some 3000 in all. There appeared to be no discernible pattern in the digits. Perhaps they had been taken from a table of random numbers. They were certainly not the opening digits of the decimal parts of π or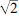 
, although they might, so far as I knew, have been consecutive digits of either number in some section remote from the decimal point.
On thinking about this, I realised that they must be the opening digits of the decimal part of the square root of some whole number. Indeed, they must be the opening digits of the decimal parts of the square roots of infinitely many positive integers. It is remarkably easy to prove this and the argument is simple enough to be appreciated and understood in school classrooms at GCSE level.
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2018
References
1. Koksma, J. F., Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins, Compositio Math. 2 (1935) pp. 250–258.Google Scholar
2. Vijayaraghavan, T., On the fractional parts of powers of a number IV, J. Indian Math. Soc. 12 (1948) pp. 33–39.Google Scholar
3. Bugeaud, Y., Distribution modulo one and Diophantine approximation, Cambridge tracts in Mathematics No.193, Cambridge University Press (2012).CrossRefGoogle Scholar