Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T06:25:10.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Anamorphoscopes another look at circle inverting mirrors

Published online by Cambridge University Press:  23 January 2015

John Sharp ,
B. G. Nickel  and
J. L. Hunt
John Sharp
Affiliation:
London Knowledge Laboratory, Institute of Education, 23-29 Emerald Street, London WC1 3QS, e-mail:[email protected]
B. G. Nickel
Affiliation:
Department of Physics, University of Guelph, Guelph ON N1G 2W1, Canada, e-mails:[email protected]; [email protected]
J. L. Hunt
Affiliation:
Department of Physics, University of Guelph, Guelph ON N1G 2W1, Canada, e-mails:[email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

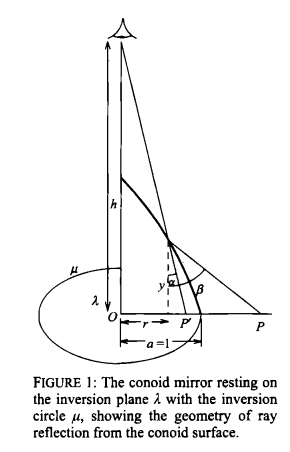
In 1979 Philip W. Kuchel published a paper [1] in the Mathematical Gazette on using curved mirrors as a means of demonstrating the transformation known as inversion in a circle. He called the mirrors ‘anamorphoscopes’ since he came to the idea as a special case of the conical mirror anamorphosis which was a popular optical toy from the seventeenth century onwards [2]. In this paper we revisit his ideas with current technology and provide some extensions to Kuchel's derivation.

Type
Articles
Information
The Mathematical Gazette , Volume 95 , Issue 532 , March 2011 , pp. 1 - 16
Copyright
Copyright © The Mathematical Association 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Kuchel, Philip W., Anamorphoscopes: a visual aid for circle inversion, Math. Gaz. 63 (June 1979), pp. 82–89.Google Scholar
2. Baltrušaitis, Jurgis (translated by Strachan, W. J.), Anamorphic Art, Abrams, New York (1977).Google Scholar
3. Hunt, J. L., Nickel, B. G., Gigault, Christian, Anamorphic Images, Amer. Journal of Physics 68 (2000) pp. 232–237.CrossRefGoogle Scholar
4. Cargo, Gerald T., Graver, Jack E., Troutman, John L., Designing a mirror that inverts in a circle, Mathematical Intelligencer, 24, pp. 4–8.Google Scholar
5. Abramowitz, and Stegun, , Handbook of Mathematical Functions Dover, New York (1970).Google Scholar
6. Kempe, A. B., How to draw a straight line: A lecture on Linkages, London (1877).Google Scholar
7. POV-Ray is available from www.povray.org Google Scholar